DISTRIBUCION DE PROBABILIDAD

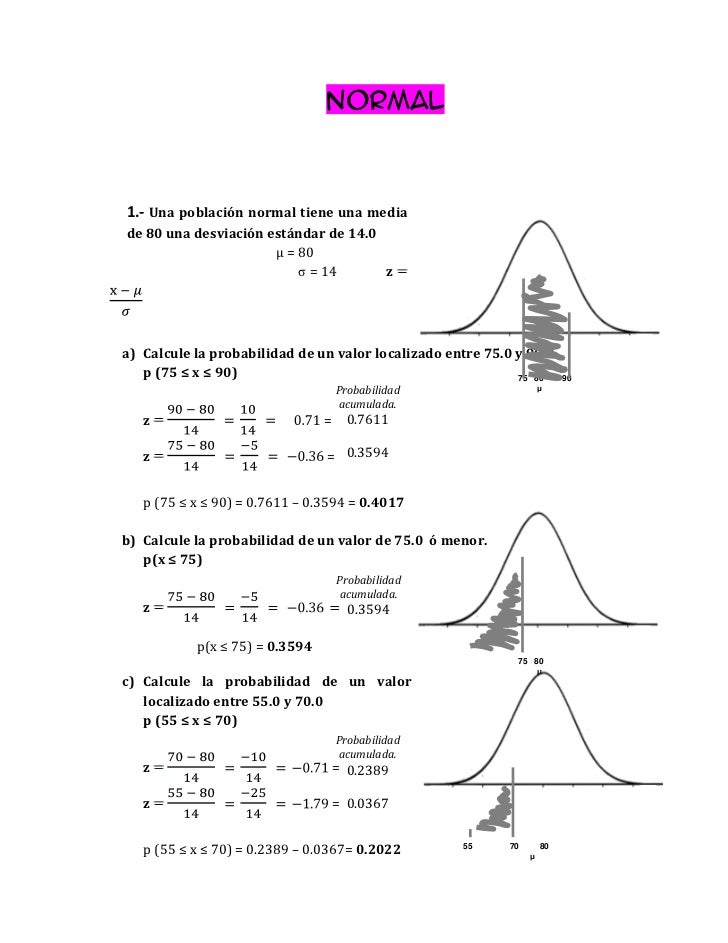
La distribución normal es posiblemente la distribución de probabilidad más conocida y más aplicada en el campo de la bioestadistica debido a que una gran cantidad muy grandes de fenómenos reales pueden explicarse mediante este modelo de probabilidad.

La distribución normal debe su origen al matemático francés Abraham De Moire, en 1733, y son figuras importantes en su desarrollo histórico Pierre Laplace, en 1744, y Carl Gauss, en 1809 y 1816. Es a través de este último que la distribución normal alcanzó mayor notoriedad,  ya que él la desarrollo como la “ley normal de los errores de mediciones” particularmente en relación a observaciones astronómicas”. La curva normal es ampliamente conocida como la curva de Gauss o “Campana de Gauss”.

La importancia de la distribución normal se debe, en primer lugar y como ya lo hemos dicho, a que muchas variables siguen, aproximadamente, un modelo de probabilidad normal y esto ha ocasionado que en las diferentes áreas del saber, su aplicación sea generalizada en relación a este hecho hay que estar alerta y evitar incurrir en el error de creer que todos los conjuntos de datos siguen una distribución normal (enfermedades), cuestión a la que se tendían en el pasado. Actualmente se conoce como una compleja variedad de casos donde el modelo normal resulta inadecuado y deben tratarse utilizando otros tipos de distribuciones, de ser asi seria erróneo el diagnostico o probabilidad de diferentes casos clínicos cuando de salud estamos hablando.

En segundo lugar, existe un resultado muy importante con la distribución de normal conocido como Teorema central de limite, El cual establece que para una muestra suficientemente grande, la media muestral X¯¯¯ sigue una distribución aproximadamente normal, independientemente del tipo de distribución que tenga la población de la cual se extrae la muestra, en este caso se engloban casos mas grandes como epidemias.

ESPERANZA VARIANZA Y DESVIACION ESTANDAR

Media, valor esperado o Esperanza matemática. Dado un experimento aleatorio, entendemos por media o esperanza matemática de una variable aleatoria asociada a dicho experimento al valor al que tiende a estabilizarse, cuando el experimento se repite un numero elevado de veces. Se nota por E(X) y es igual a la suma de los productos de cada uno de los valores de la variable aleatoria por su función de probabilidad, así:

E(X)=

---

 xif(xi)

Propiedades de la Esperanza matemática:

a) E(a)=a siendo a un valor constante.

b) E(aX)= aE(X)

c) E(a+X)= a+ E(X)

Ejemplo de Esperanza matemática. En una lotería que sólo produce beneficios al ganador, ¿Cuál creéis que debiera ser la Esperanza matemática de la variable euros ganados en dicha lotería? La solución E(X)= 0

 Varianza y desviación típica. La Varianza se define como la Esperanza matemática de los cuadrados de las desviaciones de los valores de la variable con respecto a su Esperanza matemática. Así

---

²(X) = Var(X) = E[(X-E(X))²] = E(X²)-[E(X)]² siendo la desviación típica la raíz cuadrada de la varianza

Propiedades de la varianza

  

---

²(a) = 0 siendo a un valor constante

  

---

²(a+X) =

---

²(X)

  

---

²(a•X) = a²•

---

²(X)

Variables aleatorias DICOTÓMICAS. Media y varianza de dichas variables.

Una variable aleatoria diremos que es dicotómica cuando dicha variable sólo puede tomar dos valores distintos; x1=0 y x2=1. La función de probabilidad de una variable dicotómica sería, si f(1)= p como

---

 f(xi) = 1, entonces f(0)+f(1)= 1 y como f(1)=p, tendríamos que f(0)=1-p.

La esperanza matemática de una variable aleatoria dicotómica en la que f(1)=p, sería:

E(X)= 0•(1-p) + 1•p = p

E(X²) = 0² • (1-p) + 1² • p = p y la varianza sería

---

²(X) = p - p² = p•(1 - p)

Variables aleatorias TIPIFICADAS. Media y varianza de dichas variables.

Sea X una variable aleatoria cuya media o esperanza matemática es E(X)=µ y la desviación típica

---

(X) =

---

. A partir de estos valores y de la variable aleatoria X podemos construir una nueva variable Z cuyos valores se obtiene mediante la siguiente expresión

X - µ

Z = ------

Esta nueva variable tendrá una media igual a cero y una desviación típica igual a uno.

E(Z) =E(------) = -- E(X - µ ) = -- [E(X) - µ] = 0, ya que E(X) = µ

---

²(Z) = E(z²) - [E(z)]² = E(z²) ya que E(z) = 0

luego

---

²(Z) = E(z²) = E( ------)² = E[ ------] = -- E(X - µ)² = -- •

---

² = 1

Por tanto toda variable aleatoria tipificada tiene de media cero y desviación típica uno.

Desviación típica

La desviación típica es la raíz cuadrada de la varianza y se representa por la letra σ. Para calculara se calcula la varianza y se saca la raíz. Las interpretaciones que se deducen de la desviación típica son, por lo tanto, parecidas a las que se deducían de la varianza.

Comparando con el mismo tipo de datos, una desviación típica elevada significa que los datos están dispersos, mientras que un valor bajo indica que los valores son próximos los unos de los otros, y por lo tanto de la media.

Propiedades de la desviación típica

1.    σ≥0 La desviación típica es un valor positivo, la igualdad sólo se da en el caso de que todas las muestras sean iguales.

2.    Si a todos los datos se les suma una constante, la desviación típica sigue siendo la misma.

3.    Si todos los datos se multiplican por una constante, la desviación típica queda multiplicada por dicha constante.

4.    Si se dispone de varias distribuciones con la misma media y se calculan las distintas desviaciones típicas, se puede hallar la desviación típica total aplicando la fórmula

Ejemplos:

https://www.youtube.com/watch?v=1qroTjpxbs8

Probabilidad exacta

En ciertas ocaciones se conocen todos los casos posibles y los favorables, por lo tanto se puede calcular la probabilidad exactamente. la probabilidad exacta tambien se denomina probabilidad clasica, debido a que los primeros estudios sobre probabilidades estaban basados en los juegos de azar, por ejemplo la probabilidad que salga el numero 6 en la ruleta es 1 entre 37, ya que hay 37 casos posibles y solamente un seis.

ejemplo de probabilidad relacionado en el area de la salud:

Los dos miembros de una pareja son ambos portadores de un gen recesivo para una determinada enfermedad. calcular la probabilidad de tener un hijo enfermo

HOMBRE                                        MUJER 

AA*                                                AA*

AA A*A                                         AA* A*A*

SANO         PORTADORES          ENFERMO

A GEN SANO    A*GEN DEFECTUOSO

en este caso se conoce el numero de casos posibles, que son cuatro todos con la misma probabilidad;de los cuatro casos posible solo hay uno favorable al desarrollo de la enfermedad, por lo tanto la probabilidad de tener un hijo enfermo es de 0.25

Relacion directa entre la probabilidad y la salud

La probabilidad, en relación con las ciencias de la salud, mide la frecuencia con la que ocurre un resultado, para sacar conclusiones acerca de experimentos realizados, como el estudio de la eficacia de los fármacos y el aclara miento de los factores de riesgo de los mismos. La probabilidad es un elemento indispensable para los profesionales, asi mismo permite, no solo tener fundamentos lógicos y creíbles acerca de enfermedades, fármacos, diagnósticos etc. Sino también que nos sirve para llevar un control de enfermedades contagiosas y a la vez prevenirlas. Desde esta perspectiva, los profesionales de la salud siempre buscan lo mejor para sus pacientes. Así que necesitan una información clara, verdadera y justificada que los guie por el camino correcto, al momento de escoger el mejor tratamiento para una enfermedad, reconocer los síntomas característicos de patologías, para así encontrarles cura e identificar el porqué de las enfermedades. Todo esto se logra gracias al uso de la probabilidad, porque siendo un método que nos permite analizar datos verdaderos, que se obtienen de un riguroso proceso de estudio comparativo y podemos escoger lo mejor para los pacientes, satisfaciendo sus necesidades.

Para finalizar solo queda recalcar la importancia de la probabilidad en el ejercicio de los profesionales de la salud, porque gracias a ella, se puede tener certeza y seguridad de la credibilidad del trabajo arduo que desempeñan, así pues la probabilidad es importante de modo que ha servido en el estudio de enfermedades crónicas y terminales como el sida, cáncer y otras. Por otra parte la probabilidad ha evitado muchas muertes y desastres en todos los campos de las ciencias de la salud, así mismo como participan en el diario vivir de todos los profesionales de este campo, para hacerlos excelentes en su trabajo