Media, valor esperado o Esperanza matemática. Dado un experimento
aleatorio, entendemos por media o esperanza matemática de una variable
aleatoria asociada a dicho experimento al valor al que tiende a estabilizarse,
cuando el experimento se repite un numero elevado de veces. Se nota por E(X) y
es igual a la suma de los productos de cada uno de los valores de la variable
aleatoria por su función de probabilidad, así:
E(X)=
xif(xi)
Propiedades de la Esperanza matemática:
a) E(a)=a siendo a un valor constante.
b) E(aX)= aE(X)
c) E(a+X)= a+ E(X)
Ejemplo de Esperanza matemática. En una
lotería que sólo produce beneficios al ganador, ¿Cuál creéis que debiera ser la
Esperanza matemática de la variable euros ganados en dicha lotería? La solución
E(X)= 0
Varianza y desviación típica. La Varianza se define
como la Esperanza matemática de los cuadrados de las desviaciones de los
valores de la variable con respecto a su Esperanza matemática. Así
²(X) = Var(X) = E[(X-E(X))²] = E(X²)-[E(X)]² siendo la desviación típica la raíz cuadrada de la varianza
Propiedades de la varianza
²(a) = 0 siendo a un valor constante
²(a+X) =
²(X)
²(a•X) = a²•
²(X)
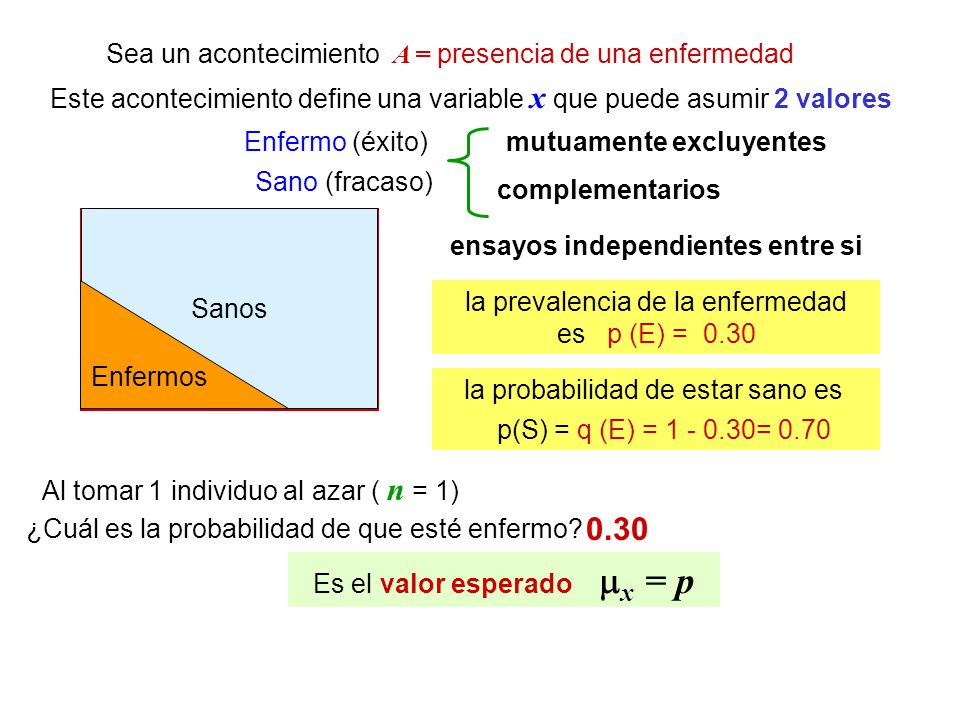
Variables
aleatorias DICOTÓMICAS. Media y varianza de dichas variables.
Una variable aleatoria diremos que es dicotómica cuando
dicha variable sólo puede tomar dos valores distintos; x1=0 y x2=1. La función
de probabilidad de una variable dicotómica sería, si f(1)= p como
f(xi) = 1, entonces f(0)+f(1)= 1 y como f(1)=p, tendríamos que f(0)=1-p.
La esperanza matemática de
una variable aleatoria dicotómica en la que f(1)=p, sería:
E(X)= 0•(1-p) + 1•p = p
E(X²) = 0² • (1-p) + 1² • p = p y la varianza
sería
²(X) = p - p² = p•(1 - p)
Variables aleatorias TIPIFICADAS. Media y varianza de
dichas variables.
Sea X una variable aleatoria cuya media o
esperanza matemática es E(X)=µ y la desviación típica
(X) =
. A partir de estos valores y de la variable aleatoria X podemos construir una nueva variable Z cuyos valores se obtiene mediante la siguiente expresión
X - µ
Z = ------
Esta nueva variable tendrá una media igual a
cero y una desviación típica igual a uno.
E(Z) =E(------) = -- E(X - µ ) = -- [E(X) -
µ] = 0, ya que E(X) = µ
²(Z) = E(z²) - [E(z)]² = E(z²) ya que E(z) = 0
luego
²(Z) = E(z²) = E( ------)² = E[ ------] = -- E(X - µ)² = -- •
² = 1
Por tanto toda variable aleatoria tipificada
tiene de media cero y desviación típica uno.
Desviación típica
La desviación típica es la raíz cuadrada de la
varianza y se representa por la letra σ. Para calculara se
calcula la varianza y se saca la raíz. Las interpretaciones que se deducen de
la desviación típica son, por lo tanto, parecidas a las que se deducían de la
varianza.
Comparando con el
mismo tipo de datos, una desviación típica elevada significa que los datos
están dispersos, mientras que un valor bajo indica que los valores son próximos
los unos de los otros, y por lo tanto de la media.
Propiedades de la desviación típica
1. σ≥0 La
desviación típica es un valor positivo, la igualdad sólo se da en el caso de
que todas las muestras sean iguales.
2. Si
a todos los datos se les suma una constante, la desviación típica sigue siendo
la misma.
3. Si
todos los datos se multiplican por una constante, la desviación típica queda
multiplicada por dicha constante.
4. Si
se dispone de varias distribuciones con la misma media y se calculan las
distintas desviaciones típicas, se puede hallar la desviación típica total
aplicando la fórmula
Ejemplos:

No hay comentarios.:
Publicar un comentario